поиск за координатами

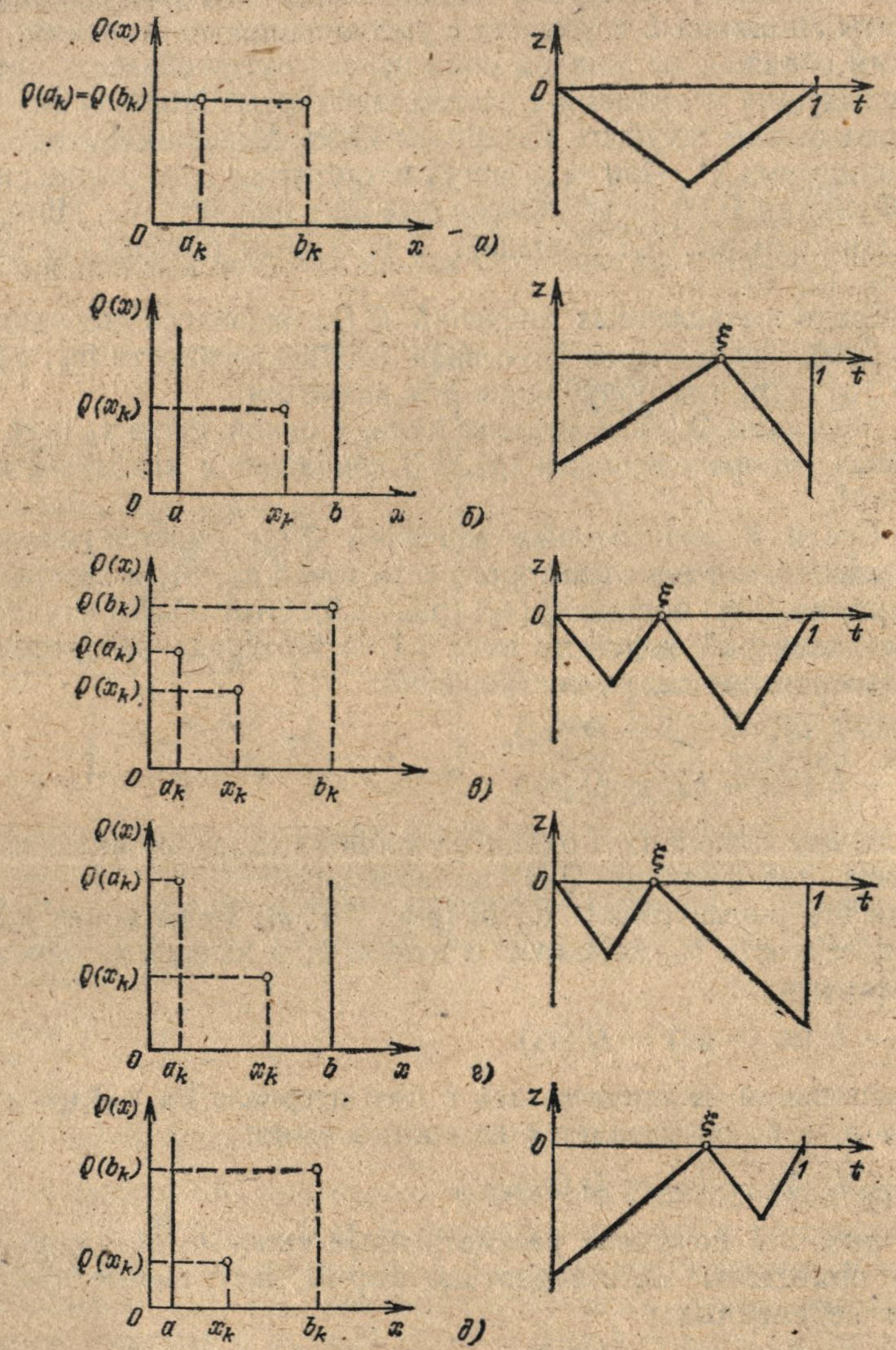
Если Q (?1) ? Q (?), то х*?[?, 1] и так как ?1 выбрано по, методу Фибоначчи, то после N испытаний получим

?1 = ? + (1 – ?)/uN-2/uN. (3.65)

Первое испытание будем проводить по методу Фибоначчи, предположив, что а = ?, b = 1 и число испытаний равно (N – 1), в точке

С другой стороны, для унимодальной функции Q (*), как было показано ранее, наилучшим является метод Фибоначчи, который гарантирует получение после N испытаний наименьшего допустимого апостериорного интервала неопределенности не меньше чем 1/uN, что больше чем (1 ?)/uN. Следовательно, мы пришли к противоречию, что и доказывает справедливость неравенства (3.63). Установим теперь справедливость противоположного неравенства

Нетрудно видеть, что построенная функция Q*(х) является унимодальной и ее минимум совпадает с точкой минимума функции Q (х). Допустим от противного, что неравенство (3.63) не выполняется, т. е. для функции Q (х), определенной на отрезке [0, 1], существует процедура поиска F, которая позволяет получить апостериорный интервал неопределенности

Пусть на отрезке [?, 1] задана произвольная унимодальная функция Q (x). Доопределим ее следующим образом:

lN(?) ? (1 – ?)/uN. (3.63)

Покажем, что в атом случае

Пусть соотношение (3.61) имеет место при (N 1)-м числе испытаний Докажем его справедливость для N испытаний, предположив, что

что и подтверждает справедливость (3 61).

позволяет получить апостериорный интервал неопределенности

1/2 + ? в противном случае}

При N = 1 испытание в точке

В связи о этим докажем справедливость только выражения (3.61).

lN(1-?) = lN(?) для 1/2 ? ? ? 1.

Соотношение (3.62) получается из (3.61) по симметрии:

lN(?) = bN – aN = max ((1-?)/uN, ?/uN-1), 0 ? ? ? 1/2; (3.61)

Без потери общности предположим, что решается задача минимизации унимодальной функции Q (х), определенной на единичном интервале [0, 1], во внутренней точке ? которого имеется информация о численном значении функции Q (?). В этом случае применение процедур сокращения интервала неопределенности позволяет получить после проведения N испытаний апостериорный интервал неопределенности [aN, bN], длина которого определяется следующим выражением:

Научные статьи для Вашей учебы на all4study.ru!

Повышение эффективности унимодального поиска за счет дополнительной информации о минимизируемой функции